قصت سلوى دوائر متطابقة من ورق مزخرف و ألصقتها على لوحة من الفلين الأبيض، كما في الشكل أدناه، ما مساحة الجزء المغطى بالورق المزخرف من لوحة الفلين؟

قصت سلوى دوائر متطابقة من ورق مزخرف و ألصقتها على لوحة من الفلين الأبيض، كما في الشكل أدناه، ما مساحة الجزء المغطى بالورق المزخرف من لوحة الفلين؟
قصت سلوى دوائر متطابقة من ورق مزخرف و ألصقتها على لوحة من الفلين الأبيض، كما في الشكل أدناه، ما مساحة الجزء المغطى بالورق المزخرف من لوحة الفلين؟.
في الهَندسِةِ الرّياضِيّةِ، الدَّائرَة هي شكلٌ هَندَسيٌّ مُستوٍ، تُعرَّفُ على أنّها المحلُّ الهندسيُّ لنقاطِ تقع على سطح مُستوٍ وتَبعدُ بُعداً ثابتاً من نقطةٍ ما. تُسمَّى هَذه المجمُوعةُ غَيرُ المُنتَهيةِ من النقاطِ مُحيط الدائرةِ أو «المُحيطُ» اختصاراً. بينما النُّقطةُ الثابتةُ تُسمَّى مركزَ الدائرةِ. وأخيراً، تُسمّى المَسافةُ من أيِّ نُقطَةٍ على المُحيطِ إلى المركزِ نصفَ قُطْرِ أو شعاعاً، والقطرُ هو قِطعةٌ مُستقيمةٌ تمرُ بمركز الدائرة وتصل بين نقطتين على المحيط. تُصنُّفُ الدائرةُ على أنَّها قطعٌ ناقصٌ تلاشت بؤرتاهُ في نُقطةٍ واحدة أو قطع مخروطي مُنعدِمُ الاختلافِ المركزيّ؛ وعلى ذلك، فإنَّ الدائرةَ قطعٌ مخروطيٌّ ينتج عن تقاطع المخروط مع مستوىً مُوازٍ لقاعدتهِ. كما عُرِّفتِ الدائرةُ بوصفها مُضلَّعاً مُنتظماً لانهائي الأضلاع.
ارتبطتِ الدائرةُ قديماً بالعديدِ منِ المسائل الرياضية، كما أنَّ لها ارتباطاً وثيقاً ببقيةِ الأشكالِ الهندسيّةِ من الزوايا والقطعِ المستقيمةِ والمُضلّعاتِ. يُطلق على المُضلعات التي توجَدُ دائرةٌ تُحيطها صفة «الدائرية»، أي أنَّ رؤوسَها مُشتَرِكَةٌ بِدَائِرَةٍ. ولهذهِ المُضلعاتُ قوانينُ ومبرهناتٌ خاصّةٌ تنطبق عليها. كانت الدائرةُ محطَّ اهتمامٍ بالأخصِّ عِندَ الإغريقِ القدماء. يَنتُجُ عن قِسْمَةِ طولِ مُحيطِ الدّائرةِ على طولِ قطرِها الثّابت الرّياضي ط.
وضع فلاسفة الأغريق القدماء نموذج مركزية الأرض الذي استندوا فيه على أنَّ الأرض كرةٌ تقع في مركز الكونِ والسماوات وتدور حولها بقية الأجرام السماوية في دوائرَ. وعندما قدَّم نيكولاس كوبرنيكوس نظرية مركزية الشمس، اعتبر أن نسيج الكون يتكون من حلقات دائرية حول الشمس. إلى أن توصَّلَ كيبلر إلى حقيقة شكل مدارات الأجرام السماوية، وهي قطوع ناقصة بدلاً من كونها دوائرَ، وحدد نيوتن الشروط التي يجب أن تتوفر في الجسم حتى يحذو مساراً دائرياً.
تُعتبرُ الدائرةُ أحد أكملِ الأشكال الهندسية وأكثرها مثاليةً، وكان لها أهميَّة في التقنية والفنون والأديان والثقافات.
تُرسَمُ الدوائرَ باستعمال الفرجار. والفرجار هو الأداة الوحيدة إلى جانب المسطرة المسموح باستخدامها في الهندسة الإقليدية؛ وهذا ما جعلها تُسمَّى «هندسة المسطرة والفرجار».
تربيع الدائرة، تثليث الزاوية ومضاعفة المُكعَّب كانت من أبرز المسائل الرياضية والمواضيع التي حاول فيها الرياضيون على مر التاريخ، إلى أن أثبت بيير وانتزل وفيردينوند فون ليندمان استحالة تِلكُمُ المسائل.
في الرياضيات، يمكن أن يُشير مصطلح "الدوائر" إلى الأشكال الهندسية المستديرة التي تتكون من مجموعة من النقاط في الفضاء، حيث تكون كل النقاط في المستوى نفسه بعدد ثابت من الوحدات المسافية عن مركز الدائرة. وهذا الوحدة المسافية تُعرف بالنصف قطر. تعتبر الدوائر من أبسط الأشكال الهندسية ولها العديد من الخصائص الفريدة، مثل قطرها ومحيطها ومساحتها ومركزها.
وتُمثل الدوائر في الرياضيات عبر المعادلات الرياضية، حيث يتم استخدام المعادلات الموجودة للدوائر لحساب أبعادها وخصائصها المختلفة. بعض المفاهيم الأساسية المرتبطة بالدوائر تشمل قطر الدائرة (الخط المار بين نقطتين على طول مركزها) ومحيط الدائرة (المسافة حول الدائرة) ومساحة الدائرة (المنطقة المحصورة داخل الدائرة).
وتُستخدم الدوائر في العديد من فروع الرياضيات والعلوم، مثل الهندسة الهندسة الفضائية والهندسة الميكانيكية وعلم البصريات وعلم الفلك والإحصاء والرياضيات التطبيقية.
مساحة الدائرة
سنتعلم الآن كيفية حساب مساحة الدائرة.
إذا كان لدينا دائرة نصف قطرها r, و وضعناها داخل مربع سنحصل على الشكل التالي:
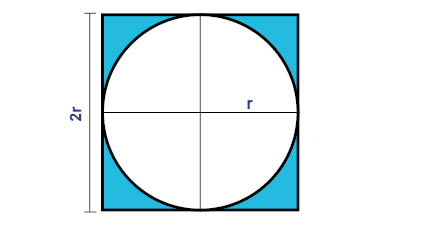
كما نعلم من قسم رُباعي الأضلاع سنحسب مساحة المربع على النحو التالي:
A_المربع = الضلع ⋅⋅ الضلع = 4r2=r⋅r⋅4=2r⋅2r4�2=�⋅�⋅4=2�⋅2�
يمكن أن نلاحظ أن هذا المربع يحتوي على أربعة مربعات صغيرة متساوية و طول ضلع كل منها r. كما نرى في الشكل مساحة الدائرة يجب أن تكون أصغر من مساحة المربع الكبير.
في الواقع مساحة الدائرة أكبر بقليل من ثلاث أضعاف مساحة أحد المربعات الصغيرة، كما هو موضح في الشكل. وبشكل أكثر تحديدا مساحة الدائرة أكبر من مساحة أحد المربعات الصغيرة بــ π� مرة (3,14 مرة).
مساحة المربع = الضلع × الضلع
عليه فإن مساحة الدائرة ستكون:
A_الدائرة = πr2=r⋅r⋅π��2=�⋅�⋅�
يمكننا استخدام صيغة مساحة الدائرة هذه لجميع الدوائر. لأن العدد π� في كل الحالات له نفس القيمة (عدد ثابت), تعتمد مساحة الدائرة على نصف قطر الدائرة فقط.
مساحة الدائرة
دائرة نصف قطرها 4 سم.
احسب مساحة الدائرة. قرب إلى رقم عشري واحد.
الحل:
نستخدم صيغة مساحة الدائرة:
A = r2⋅π�2⋅� = 42⋅π42⋅� سم2 = π16�16 سم2 ≈≈ 50,3 سم2
إذن مساحة الدائرة تساوي 50,3 سم2 تقريباً.
قطاع الدائرة
في الصف السابع في قسم الزوايا خلصنا إلى أن الدورة الكاملة تعادل °360.
وقد نريد في بعض الأحيان دراسة أجزاء من الدائرة الكاملة، كشكل شرائح التورتة مثلا، كما في الشكل أدناه:
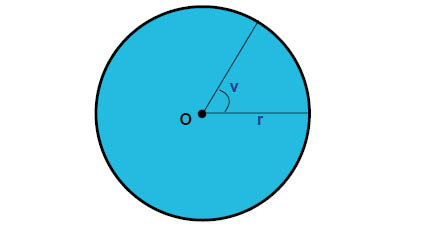
هذا النوع من أجزاء الدائرة (شكل شريحة التورتة) يُسمى قطاع الدائرة. ويعتمد حجم قطاع الدائرة على الزاوية الموجودة في منتصف الدائرة والتي نسميها الزاوية المركزية.
ويمكننا كتابة صيغة لمساحة قطاع الدائرة حيث يُشار إلى الزاوية المركزية بالحرف v:
A_قطاع الدائرة = πr2⋅v360∘��2⋅�360∘
إذا أردنا على سبيل المثال حساب مساحة قطاع دائري له زاوية مركزية v=90°�=90°, سنحصل على مساحته باستخدام هذه الصيغة:
A_قطاع الدائرة = πr2⋅14=πr2⋅90∘360∘��2⋅14=��2⋅90∘360∘
ما توصلنا إليه هو أن قطاع الدائرة الذي له زاوية مركزية v = 90° تكون مساحته ربع مساحة الدائرة. وهذا أيضا يمكننا الوصول إليه من خلال أن °90 تُمثل ربع دورة.
كم المساحة؟
دائرة نصف قطرها 10 سم. داخل الدائرة يوجد قطاع دائري زاويته المركزية °60.
احسب مساحة قطاع الدائرة. قرب إلى رقم عشري واحد.
ما هي النسبة التي تمثلها مساحة القطاع من المساحة الكلية للدائرة؟
الحل:
نعلم كل من نصف قطر الدائرة والزاوية المركزية لقطاع الدائرة. إذن يمكننا حساب المساحة باستخدام صيغة مساحة قطاع الدائرة.
A_قطاع الدائرة = 102 ⋅π⋅60∘360∘102 ⋅�⋅60∘360∘ سم2 =
= 100⋅π⋅16100⋅�⋅16 سم2 ≈≈ 52,3 سم2
إذن مساحة قطاع الدائرة هي 52,3 سم2 تقريباً.
الزاوية المركزية °60 تُشكل سُدس زاوية الدورة الكاملة (°360). وهذا يعني أن مساحة هذا القطاع تُشكل سُدس مساحة الدائرة الكاملة.
-
السؤال: قصت سلوى دوائر متطابقة من ورق مزخرف و ألصقتها على لوحة من الفلين الأبيض، كما في الشكل أدناه، ما مساحة الجزء المغطى بالورق المزخرف من لوحة الفلين؟
-
الإجابة: 256 ط سم
