الشكل المضلع يكون مغلق دائما
الشكل المضلع يكون مغلق دائما
الشكل المضلع يكون مغلق دائما
الجواب هو : صواب
ما هو الشكل المضلع؟
الشكل المضلع هو شكل هندسي ثنائي الأبعاد يتكون من مجموعة من الأضلاع المستقيمة المتصلة ببعضها لتشكل إطارًا مغلقًا. كل نقطة التقاء بين ضلعين تُسمى رأس، وكل قطعة مستقيمة تُسمى ضلع.
أنواع الأشكال المضلعة
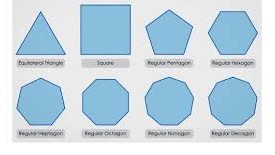
الأشكال المضلعة تختلف بعدد الأضلاع والزوايا. دعونا نتعرف على بعض الأنواع الشهيرة:
-
المثلث:
- عدد الأضلاع: 3
- عدد الزوايا: 3
- الأنواع: مثلث متساوي الأضلاع، مثلث متساوي الساقين، مثلث مختلف الأضلاع.
-
المربع:
- عدد الأضلاع: 4
- عدد الزوايا: 4
- الخصائص: جميع الأضلاع متساوية، وجميع الزوايا قائمة (90 درجة).
-
المستطيل:
- عدد الأضلاع: 4
- عدد الزوايا: 4
- الخصائص: الأضلاع المتقابلة متساوية، وجميع الزوايا قائمة (90 درجة).
-
المعين:
- عدد الأضلاع: 4
- عدد الزوايا: 4
- الخصائص: جميع الأضلاع متساوية، والزوايا المتقابلة متساوية.
-
الخماسي:
- عدد الأضلاع: 5
- عدد الزوايا: 5
-
السداسي:
- عدد الأضلاع: 6
- عدد الزوايا: 6
-
الثماني:
- عدد الأضلاع: 8
- عدد الزوايا: 8
خصائص الأشكال المضلعة
- الأضلاع: هي القطع المستقيمة التي تشكل الشكل.
- الرؤوس: هي النقاط التي تلتقي فيها الأضلاع.
- الزوايا: هي المسافات بين الأضلاع المتجاورة.
أمثلة عملية
- المثلثات: تستخدم في تصاميم الجسور والهياكل بسبب قوتها وثباتها.
- المربعات والمستطيلات: تستخدم في تصاميم الغرف والأبنية.
ما الفرق بين المضلع المحدب المضلع المقعر؟
المضلع المحدب
المضلع المحدب هو المضلع الذي تكون جميع زواياه الداخلية أقل من 180 درجة، وأي خط يصل بين نقطتين داخل المضلع يظل دائماً داخل المضلع نفسه.
خصائص المضلع المحدب:
- الزوايا الداخلية: جميع الزوايا الداخلية أقل من 180 درجة.
- الأضلاع: لا توجد أضلاع منحنية أو تنكسر إلى الداخل.
- المسافات بين النقطتين: أي خط يصل بين نقطتين داخل المضلع لن يقطع حدود المضلع.
أمثلة على المضلعات المحدبة:
- المثلثات.
- المربعات.
- المستطيلات.
- المضلعات المنتظمة (مثل السداسي المنتظم).
المضلع المقعر
المضلع المقعر هو المضلع الذي يحتوي على زاوية داخلية واحدة على الأقل أكبر من 180 درجة، وقد يكون به جزء من الخط الذي يصل بين نقطتين داخل المضلع يخرج خارج حدود المضلع.
خصائص المضلع المقعر:
- الزوايا الداخلية: هناك زاوية داخلية واحدة على الأقل أكبر من 180 درجة.
- الأضلاع: بعض الأضلاع قد تنكسر إلى الداخل.
- المسافات بين النقطتين: قد يقطع خط يصل بين نقطتين داخل المضلع حدود المضلع نفسه.
أمثلة على المضلعات المقعرة:
- نجمة خماسية.
- شكل هندسي به زاوية منحنية إلى الداخل.
الفرق الأساسي
- الزوايا الداخلية: في المضلع المحدب، جميع الزوايا الداخلية أقل من 180 درجة، بينما في المضلع المقعر هناك زاوية واحدة على الأقل أكبر من 180 درجة.
- شكل الأضلاع: الأضلاع في المضلع المحدب لا تنكسر إلى الداخل، بينما يمكن أن تنكسر الأضلاع في المضلع المقعر إلى الداخل.
- المسافات بين النقاط: أي خط يصل بين نقطتين داخل المضلع المحدب يظل دائماً داخل المضلع، بينما قد يخرج هذا الخط خارج حدود المضلع في المضلع المقعر.
مثال توضيحي
تخيل أنك ترسم مضلعين على ورقة:
- المضلع المحدب: مثل رسم مربع أو مثلث، كل الزوايا أقل من 180 درجة.
- المضلع المقعر: مثل رسم نجمة، بها زوايا منحنية إلى الداخل.
هل المضلعات اشكال مستويه؟
نعم، المضلعات هي أشكال مستوية. بمعنى أنها أشكال ثنائية الأبعاد تقع في مستوى واحد. دعنا نتحدث عن هذا الموضوع بطريقة مبسطة وممتعة:
ما هي الأشكال المستوية؟
الأشكال المستوية هي الأشكال الهندسية التي لها بُعدين فقط: الطول والعرض. هذه الأشكال توجد في مستوى ثنائي الأبعاد، مثل الورقة أو الشاشة.
تعريف المضلع
المضلع هو شكل هندسي مستوٍ يتكون من مجموعة من الأضلاع المستقيمة المتصلة ببعضها لتشكل إطارًا مغلقًا. كل نقطة تلتقي فيها الأضلاع تُسمى رأس، وكل قطعة مستقيمة تُسمى ضلع.
أنواع الأشكال المستوية
إليك بعض الأمثلة على الأشكال المستوية المضلعة:
- المثلث: 3 أضلاع.
- المربع: 4 أضلاع متساوية.
- المستطيل: 4 أضلاع، حيث الأضلاع المتقابلة متساوية.
- المعين: 4 أضلاع متساوية، ولكن زواياه ليست بالضرورة قائمة.
- الخماسي: 5 أضلاع.
- السداسي: 6 أضلاع.
- الثماني: 8 أضلاع.
خصائص الأشكال المستوية
- ثنائية الأبعاد: لها طول وعرض فقط.
- تقع في مستوى واحد: يمكن رسمها على ورقة أو أي سطح مستوٍ.
أمثلة عملية
- المثلثات: تستخدم في تصميمات الجسور بسبب قوتها الهيكلية.
- المربعات والمستطيلات: تستخدم في تصميم المباني والغرف.
تذكير بسيط
كلما تحدثنا عن الأشكال المضلعة، فإننا نتحدث عن أشكال تقع في مستوى ثنائي الأبعاد. فالمضلع هو مثال كلاسيكي على الأشكال المستوية
شروط المضلع
لتكون الشكل الهندسي مضلعاً، يجب أن تتوافر فيه الشروط التالية:
1. الشكل ثنائي الأبعاد: يجب أن يكون المضلع شكلاً ثنائي الأبعاد، أي أنه يقع في مستوى واحد وله طول وعرض فقط دون عمق.
2. الأضلاع مستقيمة: يتكون المضلع من مجموعة من الأضلاع المستقيمة. لا يحتوي المضلع على أضلاع منحنية أو دائرية.
3.الإطار المغلق: يجب أن تكون الأضلاع متصلة ببعضها لتشكل إطاراً مغلقاً. لا يمكن أن يكون المضلع مفتوحاً.
4. التقاطع عند الرؤوس فقط: الأضلاع يجب أن تلتقي فقط عند الرؤوس، ولا يمكن أن تتقاطع في أي مكان آخر غير الرؤوس.
خصائص المضلعات
إضافةً إلى الشروط، هناك بعض الخصائص التي قد تختلف من مضلع لآخر:
1. عدد الأضلاع: يمكن أن يكون للمضلع أي عدد من الأضلاع، على الأقل ثلاثة. على سبيل المثال، المثلث يحتوي على 3 أضلاع، المربع يحتوي على 4 أضلاع، وهكذا.
2. الزوايا: يتكون المضلع من مجموعة من الزوايا الداخلية. مجموع قياسات الزوايا الداخلية للمضلع يعتمد على عدد الأضلاع. صيغة حساب مجموع الزوايا الداخلية هي: \( (عدد الأضلاع - 2) \times 180 \) درجة.
3. الأضلاع المتساوية والزوايا المتساوية: بعض المضلعات تكون منتظمة، أي أن جميع أضلاعها وزواياها متساوية. المضلعات الأخرى قد تكون غير منتظمة، حيث تختلف أطوال الأضلاع وقياسات الزوايا.
أمثلة على المضلعات
- المثلث: 3 أضلاع وزوايا داخلية مجموعها 180 درجة.
- المربع: 4 أضلاع متساوية وزوايا داخلية قائمة (90 درجة) لكل زاوية.
- الخماسي: 5 أضلاع، ومجموع زواياه الداخلية 540 درجة.
- السداسي: 6 أضلاع، ومجموع زواياه الداخلية 720 درجة.
مثال توضيحي
تخيل أنك ترسم مضلعًا باستخدام قطع مستقيمة فقط وتتأكد من إغلاق الشكل بحيث لا توجد أي فجوات، وكل الأضلاع تتقاطع عند الرؤوس فقط. هذا سيكون مضلعًا صحيحًا!
